Normal curvature of an immersed surface
For curves, the curvature of a curve measure how the tangent varies, projecting onto the normal vector. But we would have obtained the same result if we had looked to the variation of the normal and projected onto the tangent.
With this in mind, for immersed surfaces $f:S\rightarrow \mathbb{R}^3$, we will consider how quickly the normal is changing along a direction and will look to the projection over this direction. That is, for a given tangent direction $X\in T_pS$ we define:
$$ \kappa_N(X):=\frac{\langle df(X),dN(X)\rangle}{|df(X)|^2} $$It corresponds to the curvature (in the sense explained in the beginning of this note) of the curve resulting of the intersection of the surface $f(S)$ with a plane containing the normal vector and the tangent $df(X)$:
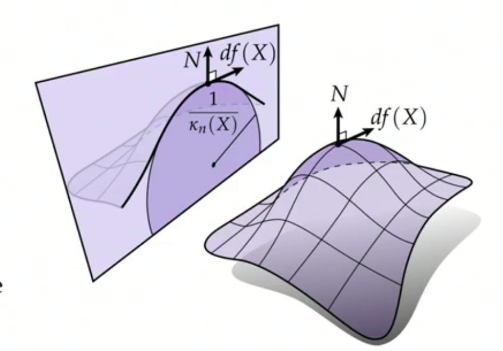
By the way, this kind of curve is called a normal section.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: